Practical Aspects of Mineral Thermobarometry

Amphiboles

Structure and sites

The amphibole structure is related to that of the pyroxenes, and consists of double chains of tetrahedra along the c axis, a pair of chains with apices facing each other forming a broad I-beam. Between the chains there are five other types of cation positions, designated M1 to M4 and A.

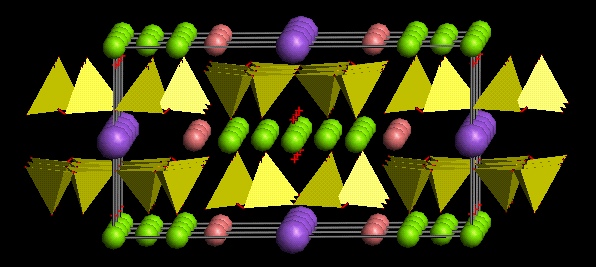
A view of the amphibole structure

The amphibole structure can be considered as interleaved modules of pyroxene and mica structure. Much of the crystal-chemical behaviour of amphiboles can be considered in this light: the M2 and M4 amphiboles sites are equivalent to the M1 and M2 sites, respectively, of the pyroxene structure. The M1 and M3 amphibole sites are like the octahedral sites in micas, and the A site resembles the mica interlayer site.

End members and site allocations

The amphibole formula unit has a large number of sites and great flexibility of substitution, but in getting familiar with the amphiboles it will help to bear in mind the comparisons indicated above with pyroxene and mica. The basic formula unit is

A_0-1 M4₂ M13₃ M2₂ T₈ O₂₂(OH)₂

where A is the large vacant or partly-filled site between the bases of chains, M13 represents the two M1 and one M3 (whose properties are very similar), and T are the tetrahedral sites. The site preferences are as follows

T (tetrahedra): Si, Al. The limit of Al substitution appears to be about 2 out of 8.
M2 (small octahedron): Al, Cr, Fe³⁺, Ti, Fe²⁺, Mg.
M1+M3 (medium octahedra): Fe²⁺, Mg, Mn.
M4 (larger cation site): Ca, Na, Mn, Fe²⁺, Mg.
A: Na, K, vacancies.

The following list contains the most commonly-used end members for monoclinic amphiboles. V is used to represent an A-site vacancy, Fe is Fe²⁺ unless expressly stated.

VCa₂Mg₅Si₈O₂₂(OH)₂ : tremolite
VCa₂Fe₅Si₈O₂₂(OH)₂ : ferro-actinolite
VCa₂Mg₃Al₂[Al₂Si₆]O₂₂(OH)₂ : tschermakite
NaCa₂Mg₅[AlSi₇]O₂₂(OH)₂ : edenite
VMg₂Mg₅Si₈O₂₂(OH)₂ : cummingtonite
VNa₂Mg₃Al₂Si₈O₂₂(OH)₂ : glaucophane
VNa₂Mg₃Fe³⁺₂Si₈O₂₂(OH)₂ : magnesio-riebeckite

A vector treatment for hornblendes, using tremolite as the base phase component, and accounting for Ti, Mn and K substitutions, might use the following set of exchange components:

Note that other commonly-used end members can be expressed as linear combinations of these, e.g. pargasite = edenite + tschermak.

Fe²⁺Mg_-1
MnMg_-1
Al₂Mg_-1Si_-1 : tschermak substitution
Fe³⁺AlMg_-1Si_-1 : ferri-tschermakite
TiAl₂Mg_-1Si_-2 : Ti-tschermak substitution *
NaAlV_-1Si_-1 : edenite vector
KAlV_-1Si_-1 : K-edenite vector
MgCa_-1 : cummingtonite vector
NaAlCa_-1Mg_-1 : glaucophane vector

* As for micas, however, it is becoming increasingly apparent that the Ti substitution probably involves Ti + 2O substituting for R²⁺ + 2OH rather than a tschermak-type exchange. Ferric iron may also substitute by this deprotonation mechanism.

Variation with grade

Because amphiboles show extensive solid solution, many aspects of their composition are controlled by the host rock chemistry. However, for hornblendes, there are a few useful grade-dependent trends:

There is a general dependence of Ti content with grade (provided there is enough Ti in the rock to saturate the amphibole). This is also reflected in the colour of hornblende in transmitted light, which varies from blue-green through green and olive green to brown with increasing grade and Ti.
At lower grades, the Al and alkali contents (edenite and tschermakite) increase markedly from near zero (tremolite-actinolite) to values more typical of hornblende (around 0.5 atoms Na+K, 2.5 atoms Al).
High contents of octahedral Al, or of Na in the M4 site, indicate relatively high pressure.
At high grade (uppermost amphibolite to granulite facies) there tends to be a relative shift, compared to lower grades, of increasing edenite and decreasing tschermakite components.

Many of the substitutions will be controlled by equilibria with other phases in the assemblage, and some of these may be sufficiently T- or P-sensitive to be of practical use in thermobarometry. Some promising examples are the hornblende-plagioclase thermometers of Holland and Blundy (1994), and the Al-in-hornblende barometer.

Formula recalculation

Because amphiboles have no fixed cation total, and may have variable OH content (so no fixed cationic charge), there is no simple method for formula and ferric iron recalculation. It is possible, however, to use crystal-chemical constraints to put limits on the possible range of Fe³⁺ contents. You can then select a "best" value centrally in this range, but remember that there is no particular significance to this mean value - all values in the permitted range are equally possible. The procedure outlined by Holland and Blundy (1994) can be used both for hornblendes and for sodic amphiboles, and is implemented in the program AX and in the spreadsheet HBAX94.

Sources and further reading

For more (much more!) on amphibole crystal chemistry see:

Robinson et al., (1981) In: Reviews in Mineralogy, 9B.
Spear (1993), pp. 90-94 and 103-105.

^ Top

This page last modified 12 October 2004

Main Sections